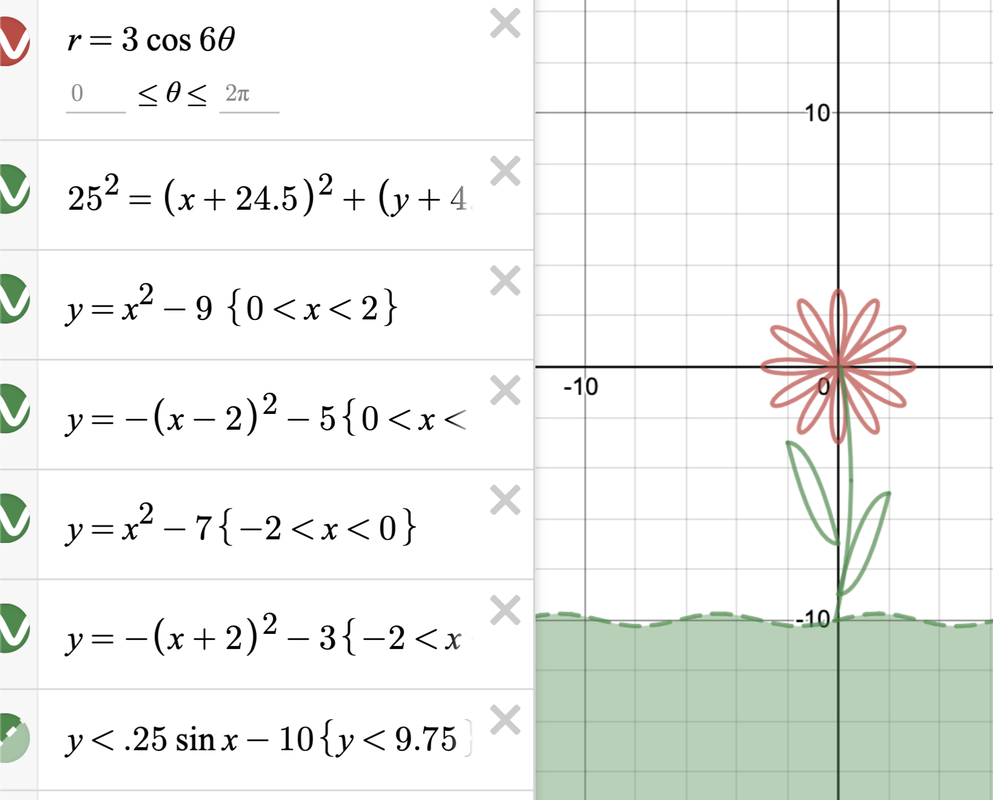
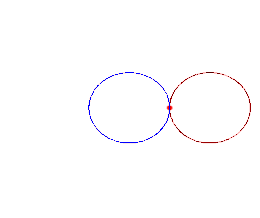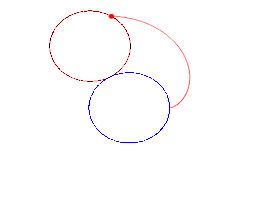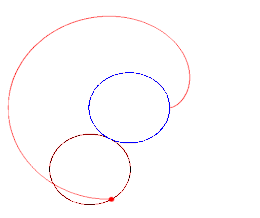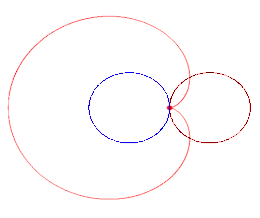
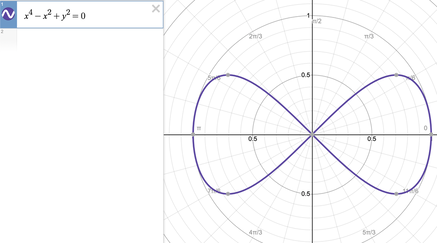
More Fun with Desmos!

My original plan was to publish another long form rant, this time about the murder of Thomas Becket in 1170 (I have a soft spot for everything related to Henry II of England). However, with all the doom and gloom we have in the news, and because while we've been self isolating in our houses, spring has arrived, I figured I'd change gears today and head back to math activities. So we're heading back to Desmos.

One of my students is prepping for the SAT, and that prep includes prep for the Math SAT II. So I've been teaching her some topics that she hasn't yet gotten to in class (and I'm nervous that with all that's going on, she WON'T get to at all), and one of these topics has been things involving trig and polar equations of all sorts.

So for anyone with a little precalc background, let's talk polar roses and their cousins.

When we talk about sine, cosine, and tangent functions and their reciprocals, we are talking about what are called periodic functions, meaning that they repeat values at regular intervals. If you plot y=sinx or y=cosx on the Cartesian (x,y) plane, you get the familiar waves that are anchored on the x-axis. 

If we graph on the polar axis, we graph in terms of r and theta (the angle measure). The polar coordinate system looks like a series of concentric circles representing r centered at the origin. This opens up a world of possibilities because coterminal angles (π/2 and 5π/2, for example) will have the same value of cosine or sine, and instead of going on forever in waves, they will be bounded by those values of r and theta. With this in mind, we can make polar roses, cardioids, and lemniscates.

Polar roses can be created using the equations r = acos(nθ) or r = asin(nθ). Just as when graphing on the Cartesian plane, the variable 'a' determines the size (amplitude) of the curve. The variable 'n' represents the b term; 2π/b determines the period (distance between repetitions of the graph). Therefore, the 'n' variable determines the number of petals your flower will have; if n is odd, the flower will have n petals, but if n is even, it will have 2n petals. Above I graphed the rose r=3cos(6θ); see how it has 12 petals? If I were to have graphed sine instead of cosine, my graph still would have had 12 petals, but it would be tilted a little because sine and cosine are phase shifts of one another.

Cardioids are technically created by rolling a fixed point on a circle around another circle of the same radius (seen below). You get a heart shaped figure as a result with a single cusp where the point returns to the beginning. Cardioids can be created with the equations r = a(1 ± cosθ) and r = a(1 ± sinθ​).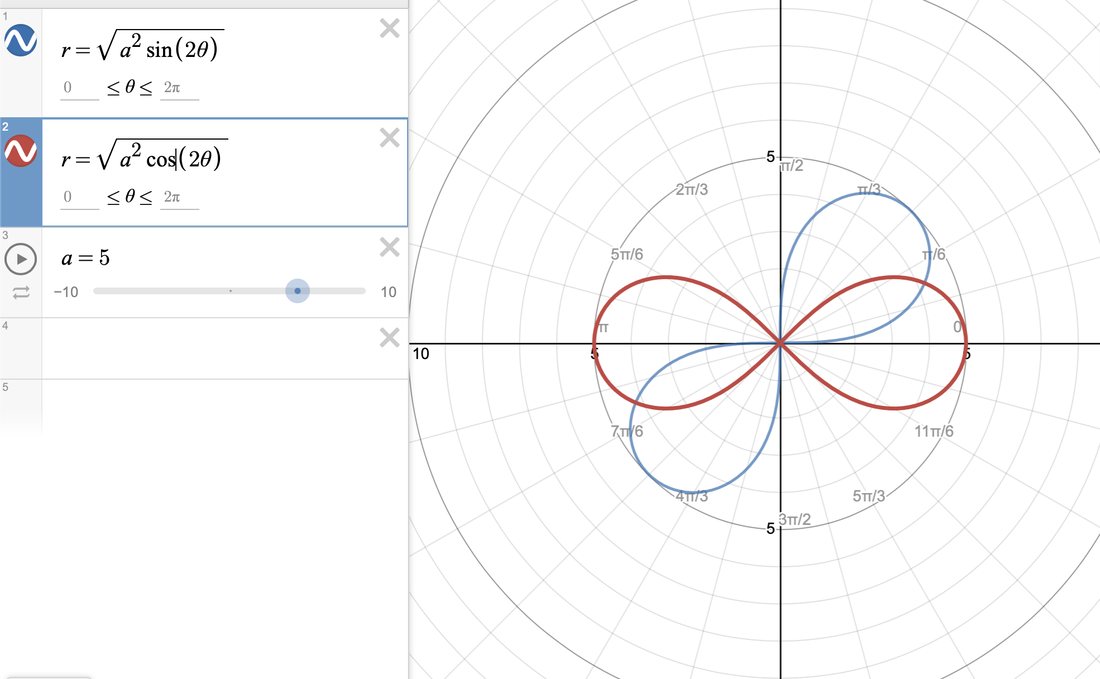

Lemniscates are a class of figure 8 or infinity symbol shaped loops. They represent all of the points (locus) whose distances from two fixed points (foci) a distance of 2a apart, when multiplied together, equal a^2. The equation for Bernoulli's leminiscate, perhaps the "classic" lemniscate, is r^2 = a^2 cos(2θ​) or r^2 = a^2 sin(2θ​) (again, tilted due to phase shift). Another famous figure 8 leminiscate (and my personal favorite) is the Lemniscate of Gerono, which has the equation x^4-x^2+y^2=0.

---

So what can you do with all of this? PLAY! I challenge you to create flowers or designs of your own using these equations. Use different values for a, b, and n and see what you get. Change your + and - signs and see your graphs flip across an axis. Combine these polar equations and come up with designs as intricate as you want. Create your own bouquet or flowers and let your imagination run wild. One of the awesome things about math is that once you add different dimensions or ways of thought to your equations, you can make shapes way cooler than a simple straight line or parabola. If you found this brief introduction interesting, I urge you to research more about these types of graphs, what they mean mathematically, and different famous forms of graphs in history because I am barely scratching the surface here. Let's brighten these dark times with some geometric flora!