Ashley's InsightsMusings on music, teaching, life, and interconnectedness. Archives
April 2020
Categories
All
|
Back to Blog
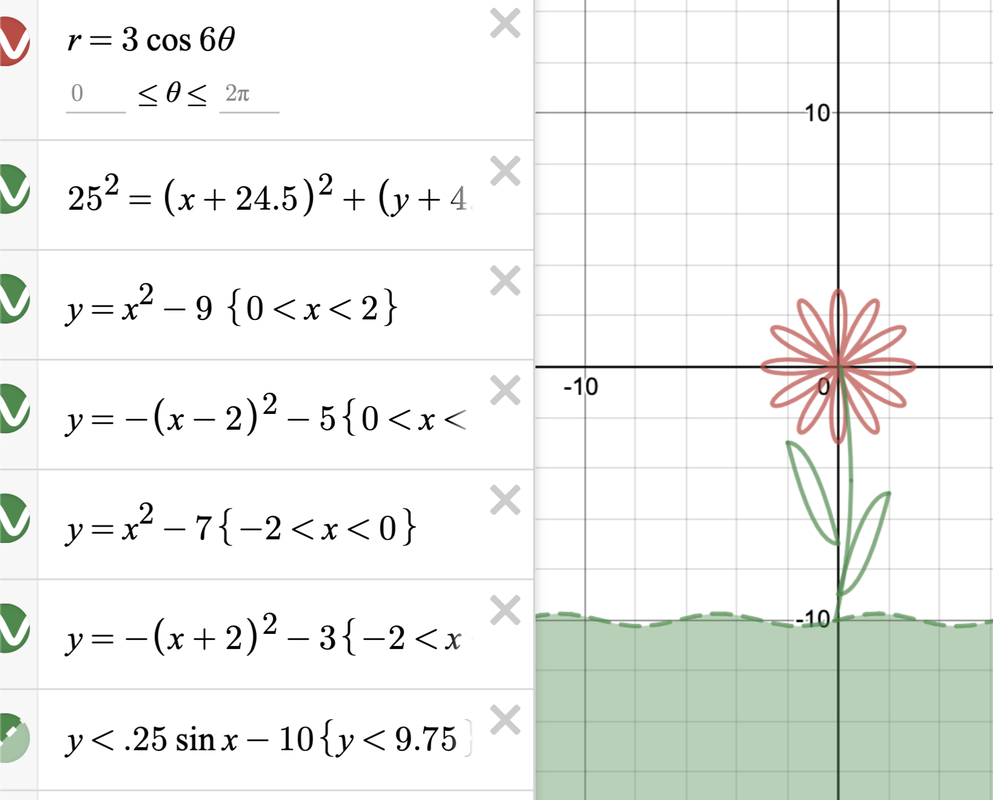
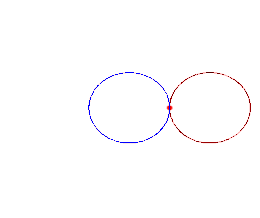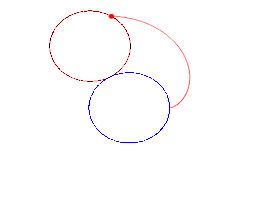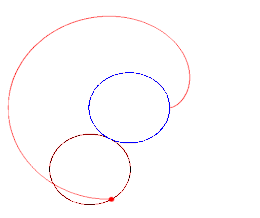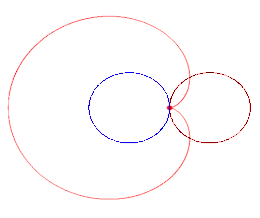
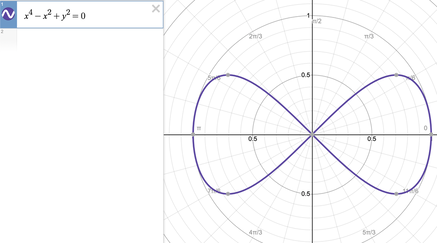
More Fun with Desmos!3/30/2020 My original plan was to publish another long form rant, this time about the murder of Thomas Becket in 1170 (I have a soft spot for everything related to Henry II of England). However, with all the doom and gloom we have in the news, and because while we've been self isolating in our houses, spring has arrived, I figured I'd change gears today and head back to math activities. So we're heading back to Desmos. One of my students is prepping for the SAT, and that prep includes prep for the Math SAT II. So I've been teaching her some topics that she hasn't yet gotten to in class (and I'm nervous that with all that's going on, she WON'T get to at all), and one of these topics has been things involving trig and polar equations of all sorts. So for anyone with a little precalc background, let's talk polar roses and their cousins. When we talk about sine, cosine, and tangent functions and their reciprocals, we are talking about what are called periodic functions, meaning that they repeat values at regular intervals. If you plot y=sinx or y=cosx on the Cartesian (x,y) plane, you get the familiar waves that are anchored on the x-axis. If we graph on the polar axis, we graph in terms of r and theta (the angle measure). The polar coordinate system looks like a series of concentric circles representing r centered at the origin. This opens up a world of possibilities because coterminal angles (π/2 and 5π/2, for example) will have the same value of cosine or sine, and instead of going on forever in waves, they will be bounded by those values of r and theta. With this in mind, we can make polar roses, cardioids, and lemniscates. Polar roses can be created using the equations r = acos(nθ) or r = asin(nθ). Just as when graphing on the Cartesian plane, the variable 'a' determines the size (amplitude) of the curve. The variable 'n' represents the b term; 2π/b determines the period (distance between repetitions of the graph). Therefore, the 'n' variable determines the number of petals your flower will have; if n is odd, the flower will have n petals, but if n is even, it will have 2n petals. Above I graphed the rose r=3cos(6θ); see how it has 12 petals? If I were to have graphed sine instead of cosine, my graph still would have had 12 petals, but it would be tilted a little because sine and cosine are phase shifts of one another. Cardioids are technically created by rolling a fixed point on a circle around another circle of the same radius (seen below). You get a heart shaped figure as a result with a single cusp where the point returns to the beginning. Cardioids can be created with the equations r = a(1 ± cosθ) and r = a(1 ± sinθ). 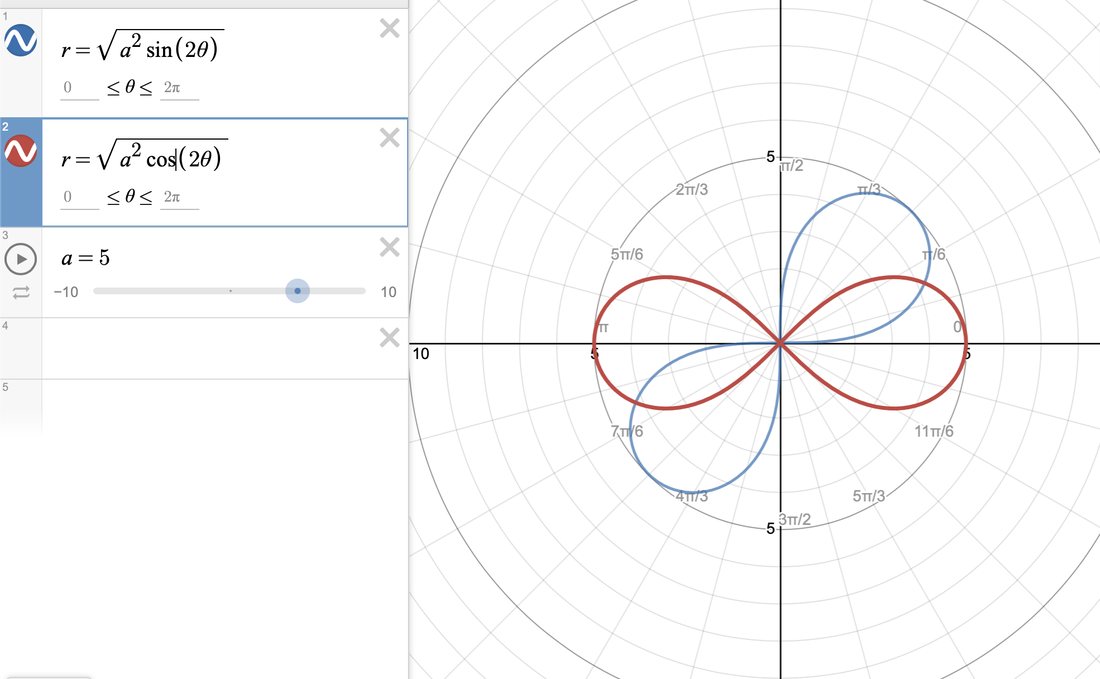 Lemniscates are a class of figure 8 or infinity symbol shaped loops. They represent all of the points (locus) whose distances from two fixed points (foci) a distance of 2a apart, when multiplied together, equal a^2. The equation for Bernoulli's leminiscate, perhaps the "classic" lemniscate, is r^2 = a^2 cos(2θ) or r^2 = a^2 sin(2θ) (again, tilted due to phase shift). Another famous figure 8 leminiscate (and my personal favorite) is the Lemniscate of Gerono, which has the equation x^4-x^2+y^2=0. So what can you do with all of this? PLAY! I challenge you to create flowers or designs of your own using these equations. Use different values for a, b, and n and see what you get. Change your + and - signs and see your graphs flip across an axis. Combine these polar equations and come up with designs as intricate as you want. Create your own bouquet or flowers and let your imagination run wild. One of the awesome things about math is that once you add different dimensions or ways of thought to your equations, you can make shapes way cooler than a simple straight line or parabola. If you found this brief introduction interesting, I urge you to research more about these types of graphs, what they mean mathematically, and different famous forms of graphs in history because I am barely scratching the surface here. Let's brighten these dark times with some geometric flora!
0 Comments
Read More
Back to Blog
The Many Marital Woes of Henry VIII3/21/2020  European history is filled with all sorts of scandals and intrigues—murders, romantic entanglements, near constant backstabbing—but few scandals in history rival England’s King Henry VIII and his six wives. After all, Henry managed (in a period of only twenty-two years) to see two wives beheaded, two marriages annulled, and the entire country of England excommunicated from the Catholic Church for his antics. The popular HBO series The Tudors romanticized much of what went on, but let’s look at what happened ourselves. When we think of Henry VIII, I’m sure many of us harken back to (at left) Hans Holbein the Younger’s infamous portrait depicting an obscenely rotund figure crowding the painting, massive codpiece screaming out, “Hey! Look at me! I’m potent and powerful!” It’s easy to make fun of such a sight five hundred years later. The real story, though, is, I think, much more tragic and certainly more complex. Henry VIII was the second son of King Henry VII, the first Tudor monarch and ruler of England after the tempestuous War of the Roses era. I’ll do more posts about this era and its illustrious personas; Margaret Beaufort, Henry VIII’s grandmother, for example, was a force of nature and deserves some recognition. As the second son, none of us should have cared much about Henry; if all had gone according to plan, he would have lived a life of relative luxury and little responsibility out of the way of political machinations of Europe at the time. Indeed, his elder brother Arthur was the child Henry VII placed all of his hopes on. In 1502, at the age of fifteen, Arthur was married to Catherine of Aragon, youngest child of the famed Ferdinand and Isabella of Spain, in order to establish an iron clad alliance between the two powers. Henry, by comparison, was a ten-year-old whose childhood was not well documented because he was just expected to be a kid. Everything went horribly wrong less than half a year after Arthur and Catherine’s marriage. An outbreak of sweating sickness swept through England, and it claimed young Arthur as a victim. At the age of ten, Henry VIII became the presumed heir to the throne and assumed the title of Prince of Wales. His father Henry VII and the Spanish diplomats in England concocted a plan for Henry to marry his brother’s now-widow, but there was a problem with this plan: according to papal law, it was illegal for a man to marry his brother’s spouse. Fortunately, Henry was so young that this wasn’t a huge issue; the Tudors appealed to the Pope for a special dispensation with the law, saying that Arthur and Catherine’s marriage was never consummated and was thus invalid, and since Henry was so young, obviously nothing seedy had happened within the families. Because British and Papal interests were aligned at the time (remember, the Vatican was as much a political entity as a religious one at that time), this was not a big deal. By the time Henry ascended to the throne in 1509 at the age of seventeen, the dispensation had been granted, and he and the now twenty-three-year-old Catherine were allowed to wed. By all accounts, Catherine and Henry had a good marriage—Henry was handsome and vigorous, Catherine bright and well-tempered. They apparently loved and trusted each other. Sure, Henry had his share of affairs on the side as was custom among the nobility of the time, fathering Henry Fitzroy with Elizabeth Blount, but all in all, the union was solid. Soon enough, they conceived their first child, but then tragedy struck. Catherine suffered a series of miscarriages, putting a strain on the marriage. Finally, in 1516, Catherine gave birth to a child who survived: the future Queen Mary. By 1525, however, Henry was impatient with Catherine. He was now well into his thirties and still did not have a male heir. Since Catherine was older than him by a few years, the probability of the two of them having a male child was growing smaller and smaller. In the meantime, Henry’s wandering eye had been captured by Anne Boleyn, sister of Henry’s mistress Mary Boleyn. Anne, unlike her sister, was known for being highly shrewd and refused to give in to Henry’s sexual advances, saying she would never be a mistress. The stage was set for one of the greatest soap operas in European history. By 1527, Henry was desperate to find a way out of his marriage to Catherine so he could pursue Anne Boleyn. However, he had been able to wed Catherine only because of a papal dispensation; the pope was not exactly happy when Henry came to him asking for an annulment of said special marriage. Up until this point, Henry was a staunch supporter of the Catholic Church; he had even been given the title Defender of the Faith by the Vatican after publishing a fervent defense of the Church (remember, this is the time of the Reformation throughout Europe). But with the pope refusing to annul his marriage to Catherine (English and Papal interests didn’t line up quite as well by this time, so the Pope was less inclined to grant Henry’s requests), Henry found himself with his hands tied. He began a series of moves that separated the Church of England from the Catholic Church, and with the Act of Supremacy in 1534, Henry made himself the sole head of the Church in England. In 1532, he banished Catherine of Aragon from court and declared that marriage invalid. Soon after, he married Anne Boleyn, who gave birth to Elizabeth I just a year later. As a result, the entire country of England was excommunicated by Rome. But alas, the marriage that was so hard fought for was not meant to be. Henry and Anne’s relationship was publicly tumultuous; Anne was intelligent and ambitious, and she was not going to play the role of subservient wife. The marriage was further strained by a series of miscarriages, the most notable happening in January 1536 after Anne learned of Henry’s severe leg wound as the result of a jousting accident. Conveniently, Henry took Jane Seymour as a new mistress at around the same time. Anne had become more of an annoyance than a help to the King, and she had to be gotten rid of. By that spring, reports were published that Anne was having multiple affairs, including one with her own brother. In sixteenth century England, this was considered treason, and in May 1536, Anne underwent a show trial, where she was found guilty of adultery and beheaded. Her child Elizabeth was, like Catherine’s daughter Mary, declared a bastard. Eleven days after Anne’s execution, Henry married his mistress Jane Seymour. By the end of the year, she became pregnant. Many believe that Jane Seymour was Henry’s favorite wife. It is certain that she was popular across England, pushing for Catherine and Anne’s children, Mary and Elizabeth, to be restored to the line of succession, and calming some of the unrest that Henry’s actions had stirred up. In October 1537, Jane gave birth to a boy, Edward VI. The labor was difficult; Edward was breech, and the labor lasted over two days. As the country celebrated the birth of the new king, Jane bled out, dying of childbirth-related complications merely days later. Henry was devastated; he did not remarry for another three years and allowed himself to become morbidly obese in the interval. When Henry died a decade later, he requested that he be buried in a grave he made himself next to Jane Seymour. In 1539, Henry’s chief minister, Thomas Cromwell, pushed for Henry to remarry and supported a union with Anne of Cleves, a German Protestant noblewoman. Cromwell was a staunch Protestant and wanted the marriage to help solidify England’s Reformation. Henry sent painter Hans Holbein to Cleves to paint a portrait of Anne so that he could see if he wanted to marry her. Holbein completed his task, delivering Henry a flattering portrait, and Henry assented to the marriage. However, when Anne arrived in England, Henry was appalled. She was relatively uneducated, only able to read and write in German, and Henry accused her of smelling poorly and having saggy breasts. He went through with the marriage, but it was never consummated, and it was, in fact, quickly annulled. Thomas Cromwell was executed for treason for pushing for the marriage, and Anne was sent away from court with a handsome financial settlement. Over time, Anne was given the title of the King’s Beloved Sister, and they actually became friendly, but the union was not to be. The day of Thomas Cromwell’s execution, Henry, now aged 49, married the eighteen-year-old Catherine Howard, a former cousin and lady-in-waiting of Anne Boleyn. Henry was suffering quite a great deal by this time; his leg wound from his jousting accident never healed (and was poorly treated by doctors at the time), he was fat, and he likely had diabetes. Catherine was young, and energetic, and mischievous. By 1541, Catherine was accused of having affairs with Thomas Culpeper, Henry’s favorite courtier, and Francis Dereham, to whom she may or may not have been engaged before marrying Henry. Love letters were found in Catherine’s handwriting addressed to Culpeper, and unlike Anne Boleyn, there is no doubt that Catherine did, in fact, commit the adultery that led to her downfall. Culpeper and Dereham were both executed at the end of 1541, and Catherine was beheaded only a few months later. Henry tried his hand at marriage one final time when he married wealthy widow Catherine Parr in 1543. Catherine was instrumental in finally getting Mary and Elizabeth restored officially in the line of succession, and Henry trusted her. They would argue over policy and religion (she was a dedicated Protestant), and when Henry traveled to France in 1544, he made Catherine regent in his stead. They never had children together, but Catherine maintained strong relationships with Henry’s children. Indeed, when Henry died in 1547, Catherine married her ex-boyfriend Thomas Seymour (Jane’s brother), and the two of them actually allowed Elizabeth to live with them for a time (until Thomas made grossly inappropriate sexual advances on Elizabeth, causing a massive scandal in its own right). It’s easy to blame Henry for being a philanderer or for being fickle, but at the root of this soap opera is a very real desire to maintain stability within England. Remember, Henry VIII was only the second Tudor monarch (and a spare at that), and his father had ascended to the throne with a very tenuous claim to it at best. Yes, he could very well be portrayed as a tyrant or as a bad king, but his reign is highly reflective of the time during which he reigned. I wouldn’t call him a victim by any stretch of the imagination, but his character is far more complex than simply “Divorced, beheaded, died. Divorced, beheaded, survived.” Understanding that complexity helps us understand the monumental shifts that Henry and his court are responsible for, and hopefully, it lets us all be a tad less dismissive of others. For more background on the Wars of the Roses and the era that Henry was born into, I highly recommend Dan Jones’s documentary series Britain’s Bloody Crown, which is available on YouTube. It ups the drama of the era maybe a bit more than necessary, but it provides decent context and will keep you or a student entertained. For more fact based research, I drew heavily from Peter Marshall’s Reformation England: 1480-1642 along with the work of David Starkey, Alison Weir, Susan Brigden, Robert Hutchinson, and my own notes from multiple British history classes with Carl Estabrook (yes, I saved them all and have them) at Dartmouth College. The BBC also has good resources for biography and context ( https://www.bbc.co.uk/teach/what-did-king-henry-vii-really-want-from-a-wife/zh9s2sg, for example).
Back to Blog
Math Enrichment: Fun with Desmos!3/21/2020 Desmos is a graphing program that's free to use online; chances are if you've got a high schooler, they've seen it. Today's educational way to stave off boredom is to draw a picture using functions! This one has been cooking for awhile; I'd love to make some sort of coloring book or paint by numbers that's truly a graph by numbers; if you plot things correctly, you get an image. It's less tedious to an artistic or creative mind.
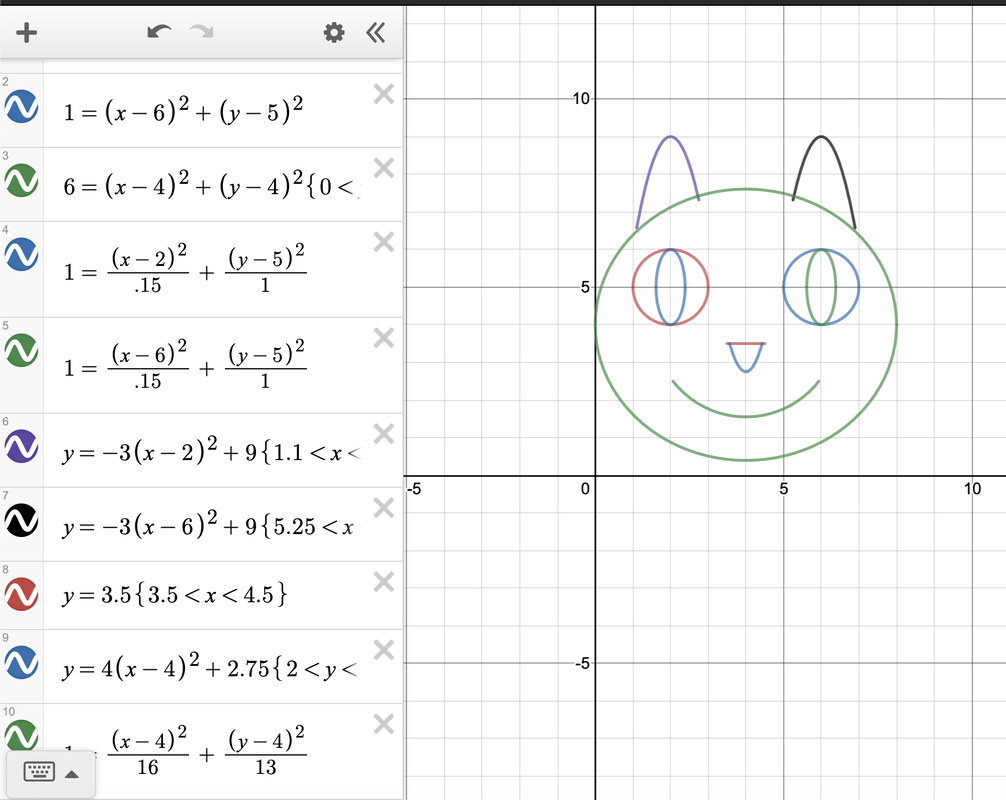
Below is a poorly drawn cat. How I made it was by inputting multiple functions (here, mostly conics because I'm working on conics with one of my students, but there's a world of possibility; go nuts!). I restricted domains (the x, or horizontal, coordinates) using brackets. For example, the top of our feline friend's nose is a horizontal line, y=3.5. How I input the function so it didn't continue past where I wanted it was by entering y=3.5{3.5<x<4.5}, which told the program that I only wanted to see those specific values. You can restrict the range (or y values) the same way. This is a simple picture, but you can be as simple or complex as your heart desires. Drawing in Desmos has multiple benefits, especially for Algebra II/Precalc students. First, it allows students to really play with transformations (shifting up and down, left and right, making things wider or more narrow). Second, it reinforces the concept of domain and range. Third, it lets students draw what they want; the world is their oyster. Again, if anyone actually tries to make a picture by plotting graphs like this, I'd love to see them.
Back to Blog
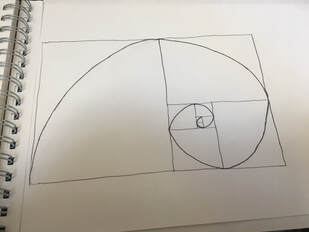
We're All In This Together3/21/2020 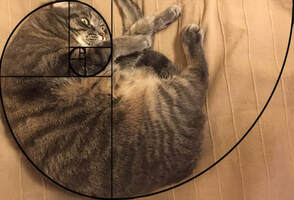 Parents with kids stuck at home: I've seen a lot of posts being like "what do I do with the kids while they're out of school and not learning?!" I get it. I'm frustrated, too, and nervous for especially high schoolers whose entire standardized testing/AP exam plans are out of whack (I'm still working both in person and remote, so if you know of students who want to learn/prep for anything, send em my way because I am experiencing disruptions and am scared). As an educator, I see this as an opportunity, though, to help reinvigorate that love of learning and creating that today's broken system has squashed. A few years ago, I started writing a book of salacious tales from history both well known and not. The idea was that I could tell the stories somewhat informally and then say "ok, if you found that interesting, here's where you can find more information". I didn't do anything with it yet because a) it's not finished and b) I'm a coward about putting my own work out there. But I'm going to start posting some of the stories here daily. It can give some kids something to research. I'm also committing to posting activities that kids of all ages can do at home to hopefully learn something and have fun. Right now I'm starting with an oldie but goodie: The Fibonacci sequence. We've all seen it before. I think my first encounter with the sequence was in a Babysitter's Club book when I was six or seven; recently it's reentered the popular imagination through the work of Dan Brown and really any TV show that wants to sound mathy. My boyfriend Erik reminded me this morning that Maynard incorporated it into Tool's Lateralus, and a quick Wikipedia search notes that the time signatures repeating reflects 987, a Fibonacci number. But what is it and why do we care about it? The Fibonacci sequence has been around in scholarly works dating back to ancient times (India, specifically), but it is named after Leonardo of Pisa, or Fibonacci, who wrote about the sequence in his 1202 book, Liber Abaci. There, he used the sequence to model rabbit population growth, but it appears in nature all the time. Look at the swirl of a seashell or the center of a sunflower or the curve of a spiral staircase; all can be fitted to the Fibonacci sequence. How does it go? Well, it's fairly simple. Each successive number in the sequence is the sum of the previous 2 numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...and so on. As the numbers get larger, dividing one number by the previous approaches what's called the golden ratio, or phi, which is an irrational number roughly equal to 1.618... You can use this ratio in many practical ways; it's used in economics to predict retracement. Hell, you can even use Fibonacci numbers and the golden ratio to loosely convert miles to kilometers and vice versa (21 miles is roughly equal to 34 kilometers). So parents, what can you do with it today with bored students? The classic move is to draw the Fibonacci spiral. Get a ruler or some graph paper. Draw a square of side length of 1. Touching one side, draw another square of side length 1. Adjacent to both, draw a square with side length of 2, then one of 3, 5, 8, and so on (I've done my own below freehand because my ruler has walked off). Draw the spiral by connecting diagonals of each square (you can use a compass if you want to be super precise). Now with the spiral drawn, you can make a variety of art projects, both realistic and abstract. The kids can learn the sequence and let their imaginations run free. If anyone makes Fibonacci art, I'd love to see it. More cool images: https://sciencevibe.com/…/the-fabulous-fibonacci-sequence-…/ |
 RSS Feed
RSS Feed